Diagonals of rhombus ABCD intersect each other at point O. Prove that OA2+ OC2=2AD2-BD2/2

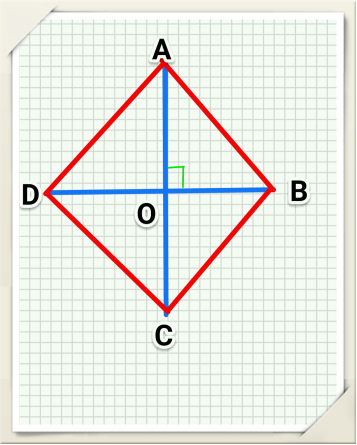
Question: Diagonals of rhombus ABCD intersect each other at point O. Prove that OA² + OC²= 2AD² + BD²/2

Solution: In &#x2206 AOD
OA² = AD² – OD² ————-Eqn (i)
In &#x2206 OBC
OC² = BC² – OB² ————-Eqn (ii)
Adding Eqn (i) & Eqn (ii) We get,
OA² + OC² = AD² – OD² + BC² – OB²
        = AD² – OD² + AD² – OB²
        = 2AD² – OD ² OB ²
        = 2AD² – (BD/2) ² -(BD/2)²
        = 2AD² – BD²/4 -BD²/4
        = 2AD² – BD²/2 Proved