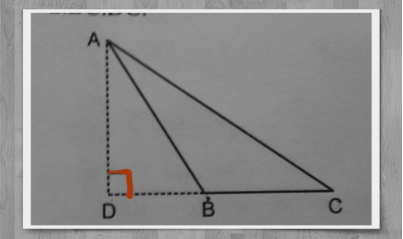
Question:In the figure AB = BC and AD is perpendicular to CD. Prove that AC2 = 2.BC. DC
solution :In ∆ ADC
AC2 = AD2 + DC2
AC2 = AB2 – BD2 + DC2(AS ABD is a right angled triangle)
or AC2 = AB2 + DC2 – BD2
AC2 = AB2 + DC2 – ( DC-BC )2
or AC2 = AB2 + DC2 – (DC2 + BC 2 -2 DC. BC)
or AC2 = AB2 + DC2 – DC2 – BC 2 + 2 DC. BC
or AC2 = AB2 – AB 2 + 2 DC. BC (As AB = BC )
.’. AC2 = 2 DC. BC Proved