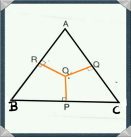
In the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC. Prove that AR² +BP² +CQ² = AQ ² + CP ²+BR²

solution :

Construction : joinA-0, BO and CO . For &#x2206 OAR, we can write:
AR² = OA² – OR² —— Eqn. (I)
For &#x2206 OBR, we can write:
BP² = OB² – OR² —— Eqn. (II)
For &#x2206 OCQ, we can write:
CQ² = OC² – OQ² —— Eqn. (III)
Adding Eqn. (I), (II) & (III) , We get:
AR² +BP² +CQ² = OA²+OB²+OC²-OR²-OP²-OQ²
        = ( OA² – OQ² ) + ( OB² -OR² ) + ( OC² -OP² )
        = AQ ² + CP ²+BR²    Proved