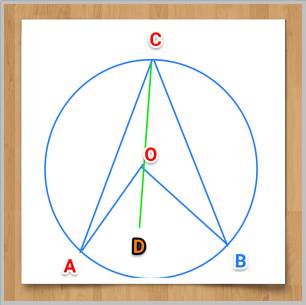
Theorem | the angle subtended by an arc of a circle | at the centre is double the angle subtended by it at | any point on the remaining part of the circle

Theorem :

A circle  with centre O in which AB subtends  &#x2220AOB at centre and angle &#x2220ACB at any point  on the remaining part of the circle.
R.T.P. – &#x2220AOB =  2 x &#x2220ACB

Solution :

Construction: Join CO and produce CO to point D .

1. In ∆AOC, OC = OA || Radii of same circle .
2. ∠OCA= ∠OAC || Base angles of isoscles &#x2206 in which OC = OA
3. Exterior &#x2220 AOD = ∠OCA+ ∠OAC || Exterior &#x2220 of a &#x2206 = sum of two opposite interior angles.
or &#x2220AOD = ∠OCA+ &#x2220OCA
or &#x2220AOD = 2 . &#x2220 OCA – – – – Eqn. 1
4. Similary ot can be proved that &#x2220BOD = 2. ∠OCB – – – – – – Eqn. 2
5. Adding Eqn 1 and Eqn. 2 we get
&#x2220AOD + &#x2220BOD = 2 . &#x2220OCA + 2. &#x2220OCB
&#x2220AOB = 2 (&#x2220OCA + &#x2220OCB)
∴ &#x2220AOB = 2 ∠ACB Proved
Video will be loaded soon.