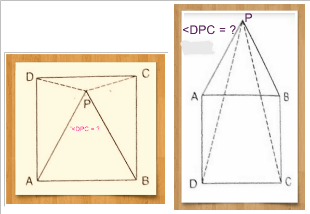
ABCD is a square and APB is an equilateral triangle.
Prove in each case:
1) 𢁪PD ≅ 𢁫PC
2) Find the angles of 𢁭PC
Solution :
First Part
Given �P = Equilateral triangle
R.T.P.
1) 𢁪PD ≅ 𢁫PC
2) Find 𢈍PC, ∠PDC and ∠PCD,
Proof: In 𢁪PD and 𢁫PC
AP = BP | Same side of the equilateral triangle.
AD = BC | Same side of the Square.
and
�P = ∠ DAB – ∠PAB = 90°-60°=300
Similarly
𢈋PC = ∠ ABC – �P = 90°-60°=30°
∴ �P = 𢈋PC
∴ 𢁪PD ≅ 𢁫PC SAS_Proved
2nd Part
In 𢁪PD
AP=AD || As AP = AB (Equilateral Triangle).
We know that �P = 30 °
∴ 𢈊PD = (180°– 30°)/2 || 𢁪PD is an isoscless ∆ and 𢈊PD is one of the base angle.
or 𢈊PD = 150°/2
or 𢈊PD = 75°
Similarly
𢈋PC = 75°
Therefore 𢈍PC = 360°– (75°+75°+60°)
or 𢈍PC = 150°
Now in ∆ PDC
PD=PC || As 𢁪PD ≅ 𢁫PC
∴ ∆PDC is an isocles ∆
And ∠PDC = ∠PCD = (180° -150°) /2
Or ∠PDC = ∠PCD = 15°
∴ ∠ DPC=150°
∠ PDC=15 °
and ∠ PCD=15 ° Answer
2nd Case proof for 2nd image and angle calculation are coming soon