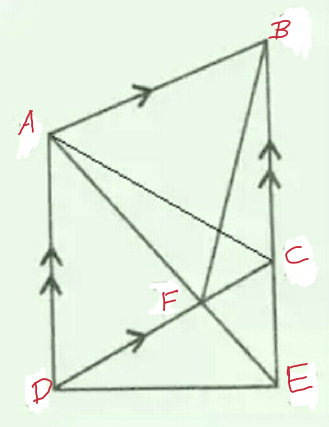
ABCD is a parallelogram , a line trhough A cuts DC at oint F and BC produced at E Prove that ∆ BCF is equal in area to ∆ DFE.
Construction: AC is joined.
AB || CD and AD || BC .
Now ∆ ACE and ∆ DCE are on the same base CE and between sane parallel lines AD and AE . Therefore
∆ ACE = ∆ DCE
∆ ACE – ∆ FCE = ∆ DCE – ∆ FCE
∴ ∆ ACF = ∆ DFE
Now ∆ ACF and ∆ BCF are on the same base and between same parallel .
∴ ∆ ACF = ∆ BCF
∴ ∆ DFE = ∆ BCF
Leave a Reply
You must be logged in to post a comment.