If    a2+b2+4c2 = ab+2bc+2ca | Expansion – Algebra

If    a²+b²+4c² = ab+2bc+2ca.    Prove that a = b = 2c

Multiplying both side by 2 we have.

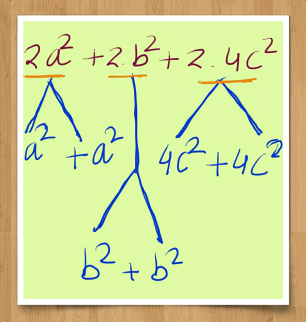
2. a² + 2. b² + 2.4c² = 2.ab + 2.2bc + 2.2ca

2. a² + 2. b² + 2.4c² = 2ab + 4bc + 4ca
2. a² + 2. b² + 2.4c² – 2ab – 4bc – 4ca =0
( a² – 2ab + b² ) + ( b² – 4bc + 4c² ) + ( a² – 4ca + 4c² ) = 0
( a – b )² + (b – c)² + (a- 2c)² = 0
If the Sum of the squares will be equal to zero then the individual terms will also be equal to zero.
∴ ( a – b )² = 0
(b – c)² = 0
and (a- 2c)² = 0
Now ( a – b )² = 0 , or ( a – b ) = 0 or a = b
Similarly (b – c)² = 0 , or (b – c) = 0 or b = c
Similarly (a- 2c)² = 0 , or (a- 2c) = 0 . or a = 2c
∴ a = b = 2c Proved